This is the homepage of Peter Alexander. I am currently at Facebook working on AR/VR. Any opinions are my own.
Recent Posts
- Single-Threaded Parallelism
- unique_ptr Type Erasure
- The Condenser Part 1
- Cube Vertex Numbering
- Range-Based Graph Search in D
All Posts
Links
github.com/Poita@Poita_
Atom Feed
Derivation of Smoothstep
Here’s the formula for smoothstep:
\[ f(t) = 3t^2 - 2t^3 \]
but where does that come from?
Oddly, when you search for “derivation of smoothstep”, none of the results are able to answer that question. So here’s my contribution to the Internet: a simple derivation of smoothstep. (To be honest, I just want an excuse to test out MathJax on my blog).
Here’s what smoothstep looks like:
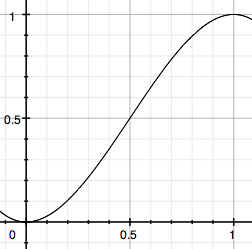
So, to start, what are we actually looking for? What are the requirements of smoothstep? Well, it starts at 0 when t is 0 and ends at 1 when t is 1, and at both those points the curve is flat, i.e. the derivative is zero. Formally:
\[
\begin{aligned}
f(0) &= 0 \\
f(1) &= 1 \\
f'(0) &= 0 \\
f'(1) &= 0 \end{aligned}
\]
That’s a good start, but there’s infinite functions that satisfy those equations. We need to restrict ourselves further. One way to do that would be to assume that the solution is a polynomial, and since there are two points where the derivative is zero we might as well assume a 3-degree polynomial (in general, a n-degree polynomial has at most n-1 critical points i.e points where the derivative is zero).
\[ f(t) = at^3 + bt^2 + ct + d \]
and the derivative is
\[ f'(t) = 3at^2 + 2bt + c \]
Substituting in the values from our formal requirements gives us a nice system of linear equations:
\[
\begin{aligned}
f(0) = 0 &\implies d = 0 \\
f(1) = 1 &\implies a + b + c = 1 \\
f'(0) = 0 &\implies c = 0 \\
f'(1) = 0 &\implies 3a + 2b = 0 \end{aligned}
\]
Solving that system of equations (manual elimination of variables is the simplest way here) gives:
\[ a = -2, b = 3, c = 0, d = 0 \]
Et voila! Plugging those back into the original polynomial gives us smoothstep.